 English English |
Bahndatenbestimmung der Venus |
| Bahndatenbestimmung der Venus Johannes Kepler (1571 - 1630) wies nach, dass sich alle Planeten des Sonnensystems auf Ellipsen um das Zentralgestirn bewegen (1. Keplersches Gesetz), die man in vielen Fällen in erster Näherung als Kreise beschreiben kann. Sitzt man als Beobachter auf dem Planet, so wirken ständig 2 Kräfte: Die Massenanziehung Sonne – Planet und die Zentrifugalkraft, die von der Kreisbewegung erzeugt wird. Beide Kräfte sind auf der Planetenbahn gleichgroß, aber entgegengerichtet. Mit diesem Kräftegleichgewicht, das für alle Planeten gilt, gelangt man zu dem 2. Keplerschen Gesetz: Die Quadrate der Bahngeschwindigkeiten verschiedener Planeten verhalten sich umgekehrt proportional zu deren Bahnradien (genauer: deren großen Halbachsen). Wendet man dies auf die Planeten Venus und Erde an, so ergibt sich (5): 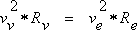 mit: Rv = Radius der Venusbahn, Ve = Bahngeschwindigkeit der Erde, Re = Radius der Erdbahn auch Astronomische Einheit (AE) genannt Den Bahnradius der Erde setze ich mit Re = 1,496*1011 m als bekannt voraus. Von den vielen Möglichkeiten zu dessen Bestimmung, die man im Internet findet, habe ich hier eine etwas leichter verständliche und humorvolle Darlegung ausgewählt: Astronomische Einheit (Copyright by Christian Flick) Mit der Erdumlaufdauer von 1 Jahr und mit der vereinfachenden Annahme einer Kreisbahn ergibt sich die Bahngeschwindigkeit der Erde zu Ve = 29,78 km/sec. Die Bahngeschwindigkeit der Venus erhält man aus der Bedeckungsstrecke vor der Sonne dividiert durch die Differenz der Kontaktzeiten t1 – t3. Die Aufgabe reduziert sich also auf die Bestimmung der Sehnenlänge (Bedeckungsstrecke), die ich aus den Transitbildern näherungsweise ermitteln konnte. Dazu habe ich mehrere Bilder zu unterschiedlichen Zeiten aufgenommen und übereinander gelegt. Folgende Grafik zeigt die Verhältnisse: 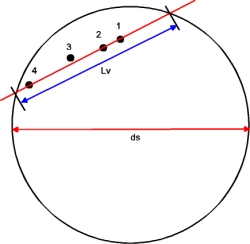 Zusammenstellung der Venuspositionen zu den Zeiten: 1: 09:10 Uhr MESZ 2: 10:19 Uhr MESZ 3: 11:36 Uhr MESZ 4: 12:44 Uhr MESZ Abb. 24: Venustransit vor der Sonne Die Länge der Sehne Lv vor der Sonne und den Durchmesser des Sonnenbildes Ds habe ich ausgemessen. Multipliziert man das Verhältnis mit dem wahren Sonnendurchmesser ds = 1,424*109 m, den ich im Jahr 2003 beim Merkurtransit ermittelt habe, so ergibt sich die wahre Strecke Ss, die die Venus vor der Sonne beschreibt (6): 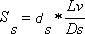 Lv = 123 mm (Sehnenlänge auf den Fotos) Ds = 165 mm (Durchmesser des Sonnenbildes auf dem Fotos) ds=1,424*109m (Sonnendurchmesser, bestimmt aus der Beobachtung des Merkurtransits 2003) Diese Aufgabe entspricht der Venus-Durchmesserbestimmung aus dem letzten Kapitel. Die vor der Sonne zurückgelegte Strecke erscheint uns als Beobachter zu groß, sie muss ebenfalls auf die Verhältnisse in der Venusbahn transformiert werden (vgl. Abb. 25). Weitere Vereinfachungen sind sinnvoll: Zunächst nehme ich an, dass die Bahnebene der Venus mit der Ekliptik zusammenfällt. Außerdem sollen die Bahnen von Venus und Erde als gerade Strecken angenommen werden, was im Rahmen der astronomischen Größenordnungen zulässig ist (siehe Fehlerbetrachtung ). 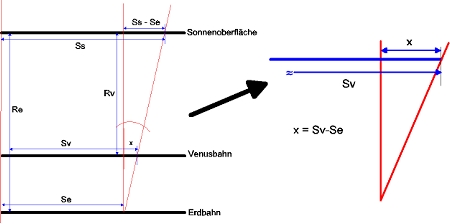 Die Grafik berücksichtigt, dass sich sowohl Erde als auch Venus bewegen. Da die Venus der Sonne näher ist, muss sie nach dem Keplerschen Gesetz eine größere Geschwindigkeit als die Erde haben. Sie legt in der Transitzeit Δt = t3 – t1 = 20 618 sec die zu ermittelnde Strecke Sv zurück. Die Erde bewegt sich in der gleichen Zeit nur um die Strecke Se. Zusammen mit der Bedeckungstrecke Ss ergibt sich ein Trapez. Aus der Länge Ss – Se errechnet man mit dem Strahlensatz die Größe x und damit die gesuchte Strecke Sv (7): 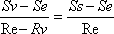 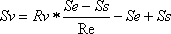 Formuliert man das Keplersche Gesetz (5) statt mit den Bahngeschwindigkeiten der Planeten Vv und Ve jetzt mit den in der Bedeckungszeit Δt zurückgelegten Weglängen Sv und Se (9): 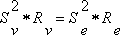 und setzt dies in Gleichung (8) ein, so ergibt sich nach wenigen Umformungen (10): 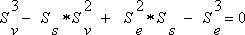 mit der Unbekannten Sv als Variable Diese Funktion 3. Grades habe ich in einer Kurvendiskussion näher untersucht: Man erhält 3 Lösungen für Sv; ein sinnvoller Wert davon ist: Sv3 = 7,9337*108 m. Dividiert man Sv3 durch die Transitzeit Δt = t1 – t3, so erhält man für die Bahngeschwindigkeit der Venus: Vv = 38,48 km/sec. Mit dem 2. Keplerschen Gesetz (5) und den bekannten Werten für die Erde findet man ihren Bahnradius Rv = 89,7 *106 km. Da die Venusbahn eine gute Kreisform hat, kann man aus Rv und Vv die Umlaufdauer mit Tv = 2πRv / Vv zu Tv = 14 647 000 sec oder 169,5 Tage ermitteln. Nach Gleichung (4) berechnet man nun auch den Venusdurchmesser zu dv = 17 270 km. In der nachfolgenden Tabelle sind meine beobachteten Größen den Literaturwerten gegenübergestellt.  Oben: Beobachtung/Berechnung Unten: Literaturwerte Als weitere Schlussfolgerung erhält man aus Gleichung (c2) (Kräftegleichgewicht) die Sonnenmasse und mit dem bekannten Sonnenradius deren Volumen und mittlere Dichte. Eine Gegenüberstellung findet man in der folgenden Tabelle.  Oben: Beobachtung/Berechnung Unten: Literaturwerte Ein Blick in Tabellenwerke zeigt, dass die Werte gute Näherungen darstellen.  Genaue astronomische Größen zu ermitteln, ist weiterhin eine Kunst. Sie müssen oft durch eine Kombination verschiedener Messverfahren auf Plausibilität überprüft werden. Die in der einschlägigen Literatur veröffentlichten, "perfekten" Bilder sind in der Regel nur mit hochgenauer und extrem teurer Ausstattung erreichbar. Demgegenüber ist es um so erstaunlicher, dass es mir gelungen ist, zu den hier aufgeführten Erkenntnissen zu gelangen. Selbst mit bescheidenen Mitteln lässt sich eine Menge über unser Sonnensystem herausfinden. Zurück zu Bestimmung der Venusgröße Zurück zu Venustransit |
|
| Copyright by Hans Joachim Ilgen seit 1950 | |