 Deutsch Deutsch |
Venus orbit data evaluation |
| Orbit data evaluation of Venus Johannes Kepler (1571 - 1630) proved that all planets of the solar system move on ellipses around the sun (first Keplerís law). In a lot of cases you ar permitted to describe them in approximation as circles. If your observer position is the planet, then two forces are constantly working: The attraction of mass between sun and planet and the centrifugal force, which is produced by the circulation. At the planets orbit both forces are equal in size and against-arranged. Assuming this force equilibrium , which can be applied to all planets, you are lead to the second Keplerís law: The squares of orbit speeds of different planets are reverse proportional to their orbit radius (more precisely: their semi-major axis). If you apply this to the planets Venus and Earth, then get (5): 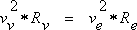 with: Vv = orbit speed of Venus, Rv = orbit radius of Venus, Ve = orbit speed of Earth, Re = orbit radius of Earth also known as astronomical unit (AU) I postulate the orbit radius of Earth with Re = 1,496*1011 m (astronomical unit AU). From a lot of Web-pages you find in internet for determining the astronomical unit, I selected a easily understandable and humorous one here:(Only in German) (copyright by Christian Flick) Using earth orbit duration of 1 year and simplifying to a circle, the orbit speed of Earth results to Ve = 29.78 km/seconds. The orbit speed of the Venus can be calculated by dividing the transit distance in front of the sun by the difference of the contact times t1 and t3. The task reduces to the determination of the chord Lv (coverage distance), which I could determine from the transit pictures. In addition I took up several pictures at different times and merged them. The following diagram shows the result: 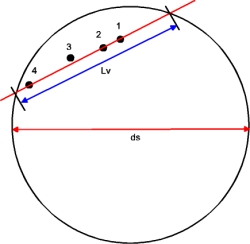 Fig. 24: Transit of Venus, merged positions Compilation of the Venus positions at the times: 1: 09:10 2: 10:19 3: 11:36 4: 12:44 o'clock (all times are Central European Summer Time, CEST) I measured the length of the chord Lv in front of the sun and the diameter of the sun picture Ds. If you multiply the ratio with the true diameter of Sun ds = 1,424*109 m, I determined from transit of Mercury in 2003, then you get the true distance Ss, which is covered by the Venus in front of the sun (6): 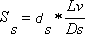
Lv = 123 mm (chord length in the photos) Ds = 165 mm (diameter of the sun picture in the photos) ds=1,424*109m (sun diameter, determined from the Mercury transit in 2003) The task corresponds to the determination of Venus diameter in the last chapter. The covering distance of Venus in front of the sun appears to large and it must be transformed likewise (see fig. 25). Further simplifications are done: First I assume that the orbit of Venus coincides with the orbit of Earth. In addition the orbits are to be accepted as straight distances, which is permitted in the context of astronomical magnitudes (see error analysis ). 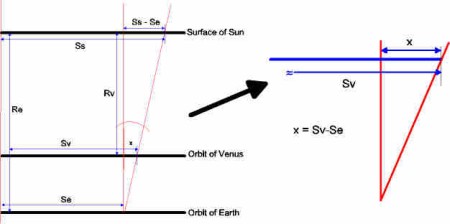 The diagram considers that Earth and Venus both move. Since the Venus is closer to the sun, it must have a larger speed than the earth according to Keplerís law. During the transit time Δt = t3 Ė t1 = 20 618 seconds it moves the distance Sv, you have to determine. The earth moves during the same time the distance Se only. Including the covering distance Ss you get a trapezoid. The quantity x is calculated from the length Ss Ė Se using the theorem on intersecting lines (7):  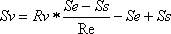 When you write Keplerís law (5) by using covering distances Sv and Se instead of speeds Vv and Ve, you get (9): 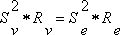 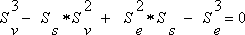 with the unknown Sv as variable. I examined this cube function using curve sketching: You receive three solutions for Sv; a suggestive value is: Sv3 = 7,9337*108 m. If you divide Sv3 by the transit time Δt = t1 Ė t3, you receive the orbit speed of Venus: Vv = 38.48 km/seconds. Assuming Earth orbit and Keplerís second law (5), you can calculate Venus orbit: Rv = 89.7 * 106 km. Since the orbit of Venus is a good circle, you can determine the time of circulation to tv = 2piRv/Vv = 14,647,000 seconds or 169.5 days. With equation (4) you compute the diameter of Venus to Dv = 17,270 km. In the following table my observed data are compared to literature values.  lower row: Literature values In further conclusions you receive from equation (c2) (force equilibrium) the solar mass and with the well-known radius of Sun its volume and medium density. The following table shows data comparison:  upper row: Observation lower row: Literature values A view into the tables shows that the values represent good approximations.  On the basis of an error analysis it shows up that astronomical data become fast inaccurate by small measuring errors and can only used as estimated values. To determine exact astronomical values, is still a matter of art. Often you have to examine the data procedures for plausibility by a combination of different measurements. The "perfect" pictures published in the relevant literature, are attainable by using precise and extremely expensive equipment only. In contrast to this, it is the amazing that I succeeded to achieve that insight specified here. Even with modest equipment you can find out a lot about our solar system. Back to determination of the Venus diameter Back to transit of Venus |
|
| Copyright by Hans Joachim Ilgen since 1950 | |