 Deutsch Deutsch |
Curve sketching |
| Curve sketching You look for zeros at the equation by the order of three (d1): 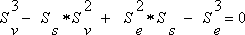
The associated function looks like type (d2): 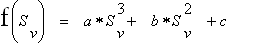
using the unknown quantity Sv where (d3): a = 1, und (d4):  and (d5): 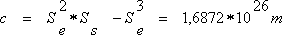
The cube function runs from - ∞ to + ∞ and you find maximally 3 zeros, 2 extrema and a turning point. You receive extreme values by the first derivative (d6): 
With the condition f'(Sv) = 0 results (d7): 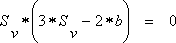
An extreme value is with Sve1 = 0 with (d8): 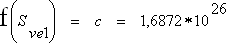
Since the curve ascends from - ∞ to a positive extremum at Sv = 0, you get the first zero at negative Sv-values (see Fig. 29 further down). The next extremum is found at (d9): 
with (d10): 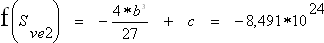
You receive the turning point Svw by the 2. Derivative with the condition (d11): 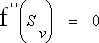
and (d12):  ,
, at the value (d13): 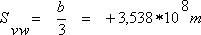
and (d14): 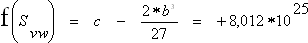
Svw is found between Sve1 and Sve2. Since f(Sve2) is negative, the last two zeros are located on the left and on the right of the second extremum. The following diagram show the process of the function. 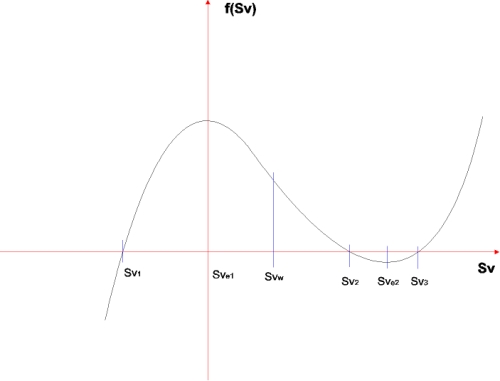 Fig. 29: function f(Sv) I determined the zeros with the program MathematikaŽ. They represent possible solutions for the Venus run. Zeros: Sv1 = -3,463 *108 m Sv2 = 6,144 *108 m Sv3 = 7,934 *108 m The solution Sv1 = -3,463 * 108 m represents a chord of a planets orbit with a triple Sun-Earth-distance, on which the planet would run in the opposite direction to earth with half orbit speed (You receive the orbit speed, by dividing the determined chords Svx by the time interval Δt = 20,618 seconds). In our solar system only the positive values Sv2 and Sv3 are realized. The solution Sv2 concerns with the cutout of the earth orbit, giving a speed Ve = 29.799 km/seconds and the solution Sv3 will be the chord of the Venus. If you divide the distance Sv3 by the time interval Δt = 20,618 seconds, you receive the unkown Venus orbit speed Vv = 38.48 km/seconds. Back to orbit data evaluation |
|
| Copyright by Hans Joachim Ilgen since 1950 | |