Der Halm einer Kornpflanze, der vom Wind angeblasen wird, knickt deshalb nicht um, weil er elastisch zurückweicht und, wenn der Wind etwas nachlässt, Schwingungen ausführt. Hat die Natur dies zufällig so gestaltet oder steckt da ein Prinzip dahinter, das auf den ersten Blick nicht erkennbar ist?

Schwingungen begegnen uns im täglichen Leben an vielen Stellen. Die meisten kennen vom Jahrmarkt die kleinen Teufel, die an Spiralfedern auf und ab schwingen. Wer genau beobachtet, sieht, dass die Wasseroberfläche, die durch einen Steinwurf eingedrückt wurde, über ihre normale Höhe hinausschnellt. An allen Musikinstrumenten schwingen kaum sichtbar Bauteile, die die Luft zu Schallwellen anregen und über unser Trommelfell im Ohr den Höreindruck erzeugen. Hochhäuser werden mit einem elastischen Stahlskelett ausgestattet, damit sie wie die Kornpflanze bei Sturm oder Erdbeben nachgeben können. In den Uhren arbeiten Unruh, Pendel oder ein Schwingquarz für eine exakte Zeit, der Fahrkomfort im Kraftfahrzeug wird durch schwingende gedämpfte Radaufhängung erhöht. Sogar Moleküle, die Atome in einem Kristallgitter und selbst die Atomkerne und deren Elementarteilchen führen Schwingungen aus und speichern auf diese Weise Energie.

Das Prinzip der Schwingung ist immer dasselbe: Elastische Objekte, die durch eine äußere Kraft aus der Gleichgewichtslage gebracht werden, schwingen, wenn sie auf die äußere Anregung mit einer rücktreibenden, ortsabhängigen Kraft reagieren. Rücktreibend bedeutet, dass die vom Objekt ausgeübte Kraft entgegengesetzt zur Richtung der anregenden Kraft wirkt. Ortsabhängig heißt hier, dass die Reaktionskraft um so größer wird, je weiter der Gegenstand aus seiner Gleichgewichtslage ausgelenkt wird.

Mit dem Sat-Roller könnt Ihr verschiedene physikalische Größen, die eine Schwingung bestimmen, experimentell messen. An diesem Versuchsaufbau lernt Ihr einiges über den Begriff der Schwingung. Und wenn Ihr das allgemeine Prinzip verstanden habt, dann könnt Ihr es auf viele unterschiedliche Bereiche in der Physik anwenden.

Wichtiges über Messtechnik erarbeitet Ihr ganz nebenbei beim Experimentieren. Die sinnvolle Durchführung der Experimente ist Voraussetzung für gute Ergebnisse. Bei jeder Messung treten Messungenauigkeiten auf, die Ihr nicht vermeiden könnt. Lässt man z. B. mehrere Personen die Höhe einer Tischplatte messen, so bekommt man verschiedene Ergebnisse (77,3 cm, 77,2 cm, 77,7 cm, 77,55 cm, 76,9 cm ...). Die Messwerte streuen um einen bestimmten Wert, den Mittelwert, der hier 77,33 cm beträgt. Der Bereich, in dem die Messergebnisse liegen, hier ± 0,4 cm, nennt man Messunsicherheit. Wenn Ihr den Bereich der Messunsicherheit angeben könnt, seid Ihr in der Lage, eine Aussage über die Genauigkeit eurer Messung zu machen. Sicherlich ist es ein Ziel, diesen Bereich so klein wie möglich zu machen.

Der Versuchsaufbau besteht aus einer parabolischen Satellitenschüssel mit den Achsenlängen 72 cm und 83 cm. Auf einem Brett wird die Schüssel auf vier in ihrer Höhe verstellbaren Spitzen gelagert. In der Satellitenschüssel kann man verschiedene Kugeln und Zylinder hin und her rollen lassen. Startet man die "Roller" am Rand, so führen sie Schwingungen aus und bleiben nach einiger Zeit im tiefsten Punkt der Schüssel liegen. Für die Versuche braucht Ihr verschiedene Gegenstände aus folgender Tabelle. Bitte überprüft zu Beginn eurer Experimente, ob alles vorhanden ist.

Eine Schwingung ist eine periodische Bewegung. Im vorliegenden Beispiel führt ein rollender Gegenstand eine Schwingung in der Satellitenschüssel aus. Für diese Bewegung gibt es eine feste physikalische Größe: Die Schwingungsdauer, die die Bewegung beschreibt und vom Aufbau der Schüssel und den Eigenschaften der verwendeten Materialien abhängt. Unter der Schwingungsdauer versteht man die Zeit, die der ausgelenkte Roller braucht, um wieder den gleichen Zustand einzunehmen. Dies können beliebige Orte, aber auch die maximalen Endlagen in der Schüssel sein.

Die Anzahl der Schwingungen, die der Roller in einer Sekunde ausführt, heißt Frequenz und wird in der Einheit [1/s] oder Hertz [Hz] gemessen. Sie kann als Kehrwert aus der Schwingungsdauer berechnet werden. Die Frequenz des Parabolantennen-Roller kann auch kleiner als 1 Hz sein. Wird das System sich selbst überlassen, so schwingt es gewöhnlich mit einer ganz charakteristischen Frequenz wie z.B. ein Pendel. Diese Frequenz nennt man Eigenfrequenz.

Die größte Auslenkung einer Schwingung nennt man Amplitude.

Die Rollgeschwindigkeit ist bei der Schwingung nicht konstant und wird durch Reibung zwischen dem Roller und der Schüsseloberfläche beeinflusst. Die Reibung bewirkt, dass die Amplitude mit der Zeit abnimmt. Es stellt sich nach einiger Zeit der Gleichgewichtszustand, nämlich die Ruhelage, gewöhnlich im tiefsten Punkt der Schüssel, ein.

Am besten führt Ihr zuerst eine Probierphase durch. Bringt die Schüssel mit den Stellschrauben und der Wasserwaage in eine waagrechte Lage. Dabei müsst Ihr darauf achten, dass die Schrauben aus dem Brett unten nicht herausragen. Der maximale Verstellweg wird durch die Brettdicke und die Höhe der Halterungsklötze bestimmt. Lasst nun je einen Roller von jeder Sorte aus bestimmten Höhen (Auslenkung) oder vom Schüsselrand in die Ruhelage rollen. Beschränkt euch dabei auf die 2 Achsen. Wie viele Schwingungen könnt Ihr bei welchem Roller beobachten? Wie lange dauert etwa eine Schwingung? Wo bleiben die Roller liegen? Steht die Größe der Auslenkung im Zusammenhang mit der Schwingungsdauer oder der Anzahl der Schwingungen?

Ihr habt jetzt eine Vorstellung davon bekommen, was mit den Rollern passiert. Nun soll aber euer Experiment genauer werden. Gute Wissenschaftler beschreiben zunächst ihren Versuchsaufbau und dann, was und wie sie gemessen haben. Ein wichtiger wissenschaftlicher Grundsatz ist die Nachprüfbarkeit eurer Ergebnisse durch andere Personen. Ihr sollt also jetzt echte Messwerte erzeugen und auch noch sagen können, wie gut diese sind.

Quantitative Messungen machen Experimente vergleichbar. Dadurch wird es auch möglich, Vorhersagen aus der Theorie zu überprüfen. Bei jeder Messung entstehen allerdings Messungenauigkeiten, die natürlich nichts mit fehlerhaftem Arbeiten zu tun haben. Erst mit der Größenangabe dieser Ungenauigkeiten kann man die Qualität der gewonnenen Messwerte beurteilen.

Folgende Messungenauigkeiten können auftreten:

Möglichkeiten zur Fehlerbegrenzung und Fehlerabschätzung:

In der Einleitung wurde es schon erwähnt: Unter der Schwingungsdauer versteht man die Zeit, die der ausgelenkte Roller braucht, um wieder den gleichen Ort einzunehmen. Je nach Startort können dies beliebige Orte in der Schüssel sein. Die Achsen sind natürlich prädestiniert.

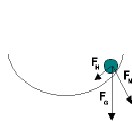
Da diese Messungen zeitkritisch sind, ist es sinnvoll, dass Ihr euch vor der Messung Gedanken zum Ablauf macht. Welche physikalischen Größen werden gemessen? Welchen Wertebereich können diese annehmen? Welche Vorbereitungen sind vor der Messung wichtig? Wie werden die Aufgaben verteilt? Wie soll die Messwerttabelle angelegt werden?

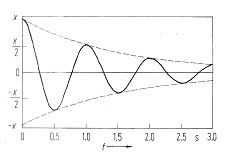
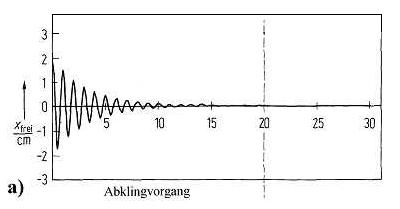
Bei den ersten Messungen an der Satellitenschüssel habt Ihr festgestellt, dass die Amplitude der Schwingung mit der Zeit abnimmt. Man nennt diese Schwingung auch gedämpfte Schwingung. In der nebenstehenden Abbildung (aus Literatur [1]) seht Ihr ein Beispiel, wie sich die Amplitude einer Rollerschwingung mit der Zeit verringert, die zu Beginn um den Wert x ausgelenkt wurde.

Der Grund für die Amplitudenabnahme der Schwingung ist die Reibung des Rollers an der Schüsseloberfläche. Durch Reibung geht Schwingungsenergie verloren, die Amplitude der Schwingung wird gedämpft. Je nach Grad der Dämpfung kann man drei Fälle unterscheiden:

Eine harmonische Schwingung entsteht, wenn - wie in der Einleitung bereits erläutert - in einem System ortsabhängige, rücktreibende Kräfte vorhanden sind. Beim Parabolantennen-Roller ist die Hangabtriebskraft, eine Komponente der Schwerkraft, als rücktreibende Kraft im Spiel. Nach dem Start des Rollers am Rand der Satellitenschüssel (Anregung der Schwingung) wandelt sich mehrfach Lageenergie (potenzielle Energie) des Rollers in Bewegungsenergie um.

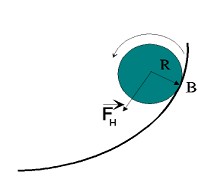
Die potenzielle Energie folgt aus der Potenzialfunktion, die Ihr bis auf einen konstanten Faktor (Gewichtskraft der Rollgeräte) bei der Vermessung der Schüsseloberfläche schon bestimmt habt. Physikalisch betrachtet ist ein Potenzial ein Vorschrift, aus der sich Energiewerte berechnen lassen. Bewegt Ihr einen Gegenstand auf der Schüsseloberfläche zwischen zwei Punkten mit unterschiedlicher Höhe (unterschiedlichem Potenzial), so müsst Ihr ihn entweder hinaufschieben und dabei Arbeit verrichten, oder hinab bewegen, wobei Arbeit frei wird. Diese Arbeit ist gleich der potenziellen Energie, die den Roller auch in Bewegung versetzen kann, wenn man ihn frei rollen lässt. Dabei erzeugt die Hangabtriebskraft über den Hebelarm Schwerpunkt - Auflagepunkt (Radius R), eine Drehbewegung. Der Roller rotiert um seinen Schwerpunkt, der sich dabei im Abstand R über der Schüsseloberfläche auf deren tiefsten Punkt zu bewegt. Die Rotation kann als Bewegungsenergie des Rollers aufgefasst werden. Analog zur Trägheit einer linearen Bewegung wirkt bei der Drehbewegung eines Körpers das Trägheitsmoment Θ.

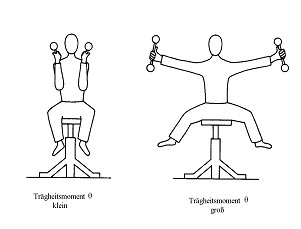
Wer einen Drehstuhl besitzt, kann ein einfaches Experiment durchführen, um die Wirkung des Trägheitsmomentes zu erfahren. Begebt euch auf einen Drehstuhl, streckt Arme und Beine aus, um Schwung zu holen und versetzt euch in Rotation (rechtes Teilbild). Dann zieht Ihr Arme und Beine dicht an euren Körper (linkes Teilbild). Was beobachtet Ihr? Zur Wiederholung könnt Ihr Arme und Beine erneut ausstrecken.

Das Trägheitsmoment ist eine Größe, die die Verteilung der Masse bezüglich ihrer Drehachse berücksichtigt (ausgestreckte, angelegte Arme bzw. Beine). Zur Bestimmung des Trägheitsmomentes wird jedes Masseteilchen mit dem Quadrat des Abstandes von seiner Drehachse gewichtet. Betrachtet man ein Massestück im Abstand R₁ und ein anderes gleich großes im Abstand 2 * R₁ von ihrer Drehachse, so besitzt die letztere Masse das 4-fache Trägheitsmoment. Je größer das Trägheitsmoment eines Körpers ist, d.h. je weiter entfernt sich seine Masse von ihrer Drehachse befindet, um so schwerer lässt sich ein Körper in Rotation versetzen. Besitzen zwei Körper gleicher Masse aber mit unterschiedlichem Trägheitsmoment die gleiche Rotationsenergie, so rotiert der Körper mit größerem Trägheitsmoment langsamer um seine Drehachse.

Als dritter Energieanteil ist die Verlustenergie zu nennen. Rollen Kugel oder Zylinder über die Schüsseloberfläche, so wandelt sich am Auflagepunkt bei jeder Schwingung ein Teil ihrer Energie durch die Rollreibung in Wärmeenergie um. Diese wird an die Umgebung abgegeben und geht dem System verloren. Der Verlust zeigt sich in der Amplitudenabnahme, die Ihr schon beobachtet habt.

Das Verhältnis von gespeicherter Energie zur Verlustenergie nennt man Güte Q des schwingungsfähigen Systems.

Die Satellitenschüssel ist an ihrer Längsachse auf zwei Spitzen gelagert und wird an der Querachse auf einer Seite mit dem Motor und dem Excenterrad, das eine Drehbewegung in eine lineare Bewegung umwandelt, angetrieben. Eine vorgespannte Feder auf der Gegenseite sorgt dafür, dass die Schüssel immer an dem Excenterrad anliegt. Die Umdrehungszahl des Motors kann durch Verändern der Motorspannung in einem ausreichenden Bereich variiert werden.

Mit dieser Anordnung kann man die Satellitenschüssel um eine Achse periodisch auf und ab bewegen und die Schwingung der Rollgeräte über einen längeren Zeitraum aufrechterhalten.

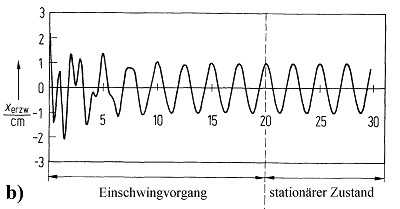
Die in eine Richtung kippbare Satellitenschüssel und die darin in gleicher Richtung rollenden Zylinder bzw. Kugeln bilden zwei schwingfähige Systeme, die sich jeweils mit unterschiedlichen Frequenzen oder Schwingungsdauern bewegen können. Nach dem Superpositionsprinzip überlagern sich diese beiden Schwingungen, die Auslenkungen addieren sich zu jedem Zeitpunkt. Startet man den Roller an einer beliebigen Stelle der Schüssel, so schwingt er in seiner Eigenfrequenz, die durch die Dämpfung eine Amplitudenabnahme erfährt. Wenn die gesamte Schwingenergie aufgebraucht ist, bleibt das Rollgerät am tiefsten Punkt der Satellitenschüssel liegen (Abklingvorgang: Abb. a). Schaltet man zwischenzeitlich den Antrieb ein, so überlagert sich die Eigenschwingung des Rollers mit der Anregung durch den Motor und der Roller führt komplizierte Bewegungsformen aus, die auch als Einschwingvorgang einer erzwungenen Schwingung bezeichnet werden (vgl. Abb. b). Ist die Anfangsenergie des Rollers weggedämpft und arbeitet der periodische Antrieb gleichförmig weiter, so stellt sich ein stationäres Verhalten ein (rechter Abschnitt in Abb. b). Immer, wenn sich die Amplitude, Phase oder Frequenz eines der Schwingsysteme ändern, so treten diese Einschwing- bzw. Abklingvorgänge auf; wartet man danach eine Weile, so hat man wieder ein stationäres Verhalten.

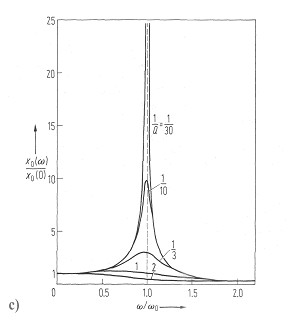
Erhöht man die Drehzahl des Motors von niedrigen zu höheren Werten, so schwingt der Roller nach der entsprechenden Wartezeit stationär mit einer von der Anregung abhängigen Amplitude. Erreicht man die Eigenfrequenz des Schüssel-Roller-Systems, so nimmt die Amplitude ein Maximum an. Man spricht dann von Resonanz. Je geringer die Dämpfung oder je größer die Güte Q des Systems, um so höher und um so schmaler ist die Amplitudenkurve als Funktion der Anregungsfrequenz (vgl. Abb. c; Resonanzkurve). Wenn die Anregungsfrequenz wesentlich über der Eigenfrequenz des Rollers liegt, dann fällt die Amplitude wieder ab.

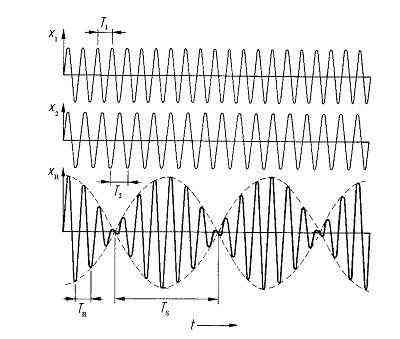Neben der Resonanz gibt es einen weiteren besonderen stationären Zustand: Die Schwebung.

Diese tritt für den Fall auf, dass der Frequenzunterschied zwischen der Anregung und der Rollbewegung gering und die Güte des Systems besonders hoch ist. In der nebenstehenden Abbildung sind zwei Schwingungen mit dem Verhältnis T₁/T₂ = 7/6 überlagert. Als Resultierende ergibt sich eine Schwingung, deren Amplitude mit der Schwingungsdauer T_S moduliert ist. Je geringer der Abstand von Anregungsfrequenz und Eigenfrequenz ist, um so größer ist die Schwingungsdauer T_S der Schwebung. Gleichzeitig verändert sich die eingehüllte Schwingungsdauer T_R der Rollerschwingung proportional zum Kehrwert der Summe aus Anregung und Eigenfrequenz.