 Englisch Englisch |
U-Rohr-Schwinger |
|
1. Einleitung 
Ein schlanker, hoch gewachsener Baum, vom Sturm angeblasen, bricht deshalb nicht ab, weil er elastisch zurückweicht und, wenn der Wind etwas nachlässt, Schwingungen ausführt. Ist das eine Laune der Natur oder steckt da ein nicht auf den ersten Blick erkennbares Prinzip dahinter?
Schwingungen begegnen uns im täglichen Leben an vielen Stellen. Die Kinderschaukel kennt jeder. Aber auch die Saite einer Gitarre, eine Stimmgabel oder die Membran einer Trommel erzeugen kaum sichtbare Schwingungen, die die Luft zu Schallwellen anregen und über unser Trommelfell im Ohr den Höreindruck erzeugen.
Die Technik nutzt das Pendel oder die Unruh, um exakte Zeitgeber herzustellen, oder die schwingende Radaufhängung, um bei einem Kraftfahrzeug den Fahrkomfort zu erhöhen. Sogar Moleküle, die Atome in einem Kristallgitter und selbst die Atomkerne führen Schwingungen aus und speichern auf diese Weise Energie.
Das Prinzip der Schwingung ist immer dasselbe:
Elastische Objekte, die durch eine äußere Kraft aus der Gleichgewichtslage gebracht werden, schwingen, wenn sie auf die äußere Anregung mit einer rücktreibenden, ortsabhängigen Kraft antworten. Rücktreibend bedeutet, dass die vom Objekt ausgeübte Kraft entgegengesetzt zur Richtung der anregenden Kraft wirkt. Ortsabhängig heißt hier, dass die Antwortkraft um so größer wird, je weiter der Gegenstand aus seiner Gleichgewichtslage ausgelenkt wird.
Mit dem U-Rohr-Schwinger sollt Ihr verschiedene physikalische Größen, die eine Schwingung bestimmen, experimentell messen. An diesem Versuchsaufbau könnt Ihr einiges über den Begriff der Schwingung lernen. Und wenn Ihr das allgemeine Prinzip verstanden habt, dann könnt Ihr es auf viele unterschiedliche Bereiche in der Physik anwenden.
Beim Experimentieren lernt Ihr auch ganz nebenbei einiges über Messtechnik. Zunächst ist eine sinnvolle Durchführung der Experimente Voraussetzung für gute Ergebnisse. Bei jeder Messung treten Messungenauigkeiten auf, die Ihr nicht vermeiden könnt. Lässt man z. B. mehrere Personen die Sitzhöhe eines Stuhles messen, so bekommt man verschiedene Ergebnisse (46,3 cm, 46,2 cm, 46,7 cm, 46,55 cm, 45,9 cm ...). Die Messwerte streuen um einen bestimmten Wert, den Mittelwert, der hier 46,33 cm beträgt. Der Bereich, in dem die Messergebnisse liegen, hier ± 0,4 cm, nennt man Messunsicherheit. Wenn Ihr den Bereich der Messunsicherheit angeben könnt, seid Ihr in der Lage, eine Aussage über die Genauigkeit eurer Messung zu machen. Sicherlich ist es ein Ziel, diesen Bereich so klein wie möglich zu machen.
2. Versuchsgegenstände Der Versuchsaufbau besteht aus einem U-Rohr aus Glas mit einer Schenkellänge von 70 cm. Das U-Rohr wird mit Wasser oder einer anderen geeigneten Flüssigkeit gefüllt. Weiterhin stehen zur Verfügung:
Bitte überprüft, ob alle Gegenstände vor Beginn eurer Experimente vorhanden sind.
3. Definitionen und Begriffe Eine Schwingung ist eine periodische Bewegung. Im vorliegenden Beispiel schwingt eine Flüssigkeitssäule in einem U-Rohr. Für diese Bewegung gibt es eine feste physikalische Größe: Die Schwingungsdauer, die die Bewegung beschreibt und vom Aufbau des U-Rohrs und den Eigenschaften aller verwendeten Materialien abhängt.
Unter der Schwingungsdauer versteht man die Zeit, die die ausgelenkte Flüssigkeitssäule braucht, um wieder den gleichen Zustand einzunehmen. Dies können beliebige Höhen, aber auch die maximalen Endlagen im U-Rohr sein. Die Anzahl der Schwingungen, die die Flüssigkeitssäule in einer Sekunde ausführt, heißt Frequenz und wird in der Einheit [1/s] oder Hertz [Hz] gemessen. Sie kann als Kehrwert aus der Schwingungsdauer berechnet werden. Die Frequenz des U-Rohr-Schwingers kann auch kleiner als 1 Hz sein. Wird das System sich selbst überlassen, so schwingt es gewöhnlich mit einer ganz charakteristischen Frequenz wie z.B. eine Pendeluhr. Diese Frequenz nennt man Eigenfrequenz.
Die größte Auslenkung einer Schwingung nennt man Amplitude.
Die Strömungsgeschwindigkeit ist bei der Schwingung nicht konstant und wird durch Reibung z. B. an der Rohrwand beeinflusst. Diese Reibung bewirkt, dass die Amplitude mit der Zeit abnimmt. Es stellt sich nach einiger Zeit wieder der Gleichgewichtszustand, nämlich die Ruhelage, ein.
4. Erste Beobachtungen Am besten führt Ihr zuerst eine Probierphase durch. Füllt das U-Rohr zunächst etwa bis zur Hälfte mit Wasser. Lenkt durch Reinblasen oder durch Ansaugen die Flüssigkeitssäule aus ihrer Gleichgewichtslage aus und lasst sie schwingen. Wie viele Schwingungen könnt Ihr beobachten? Wie lange dauert etwa eine Schwingung? Steht die Größe der Auslenkung im Zusammenhang mit der Schwingungsdauer oder der Anzahl der Schwingungen?
Ihr habt jetzt eine Vorstellung davon bekommen, was mit der Flüssigkeit passiert. Nun soll aber Euer Experiment genauer werden. Gute Wissenschaftler beschreiben zunächst Ihren Versuchsaufbau und dann, was und wie sie gemessen haben. Ein wichtiger wissenschaftlicher Grundsatz ist die Nachprüfbarkeit eurer Ergebnisse durch andere Personen. Ihr sollt also jetzt echte Messwerte erzeugen und auch noch sagen können, wie gut diese sind.
5. Allgemeine Informationen Quantitative Messungen machen Experimente vergleichbar. Dadurch wird es möglich, Vorhersagen aus der Theorie zu überprüfen. Bei jeder Messung entstehen allerdings Messungenauigkeiten, die natürlich nichts mit fehlerhaftem Arbeiten zu tun haben. Erst mit der Größenangabe dieser Ungenauigkeiten kann man die Qualität der gewonnenen Messwerte beurteilen.
Folgende Messungenauigkeiten können auftreten:
Möglichkeiten zur Fehlerbegrenzung und Fehlerabschätzung:
In der Einleitung wurde es schon erwähnt: Unter der Schwingungsdauer versteht man die Zeit, die die ausgelenkte Flüssigkeitssäule braucht, um wieder den gleichen Zustand einzunehmen. Dies können beliebige Höhen im U-Rohr sein.
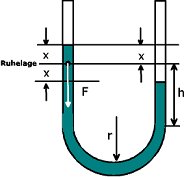 6.1 Aufgaben zur Schwingungsdauer
6.1 Aufgaben zur Schwingungsdauer
Es scheint auf der Hand zu liegen, dass die Art der Flüssigkeit einen Einfluss auf die Schwingungsdauer hat.
Um dies zu prüfen, müsst Ihr Messungen an Flüssigkeiten mit unterschiedlichen Eigenschaften durchführen.
Wie Ihr oben schon festgestellt habt, bestimmen Dichte und Zähigkeit die Eigenschaft der Flüssigkeit. Zieht man als Auswahlkriterien zusätzlich die leichte Herstellbarkeit, das Gesundheitsrisiko und das Reinigen des U-Rohrs heran, dann bieten sich Zuckerlösungen in unterschiedlichen Konzentrationen zum Experimentieren an.
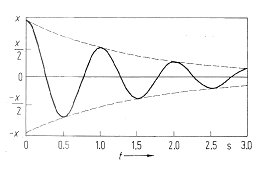
Bei den ersten Messungen am U-Rohr habt Ihr festgestellt, dass die Amplitude der Schwingung mit der Zeit abnimmt. Man nennt diese Schwingung auch gedämpfte Schwingung. In der nebenstehenden Abbildung (aus Literatur [1]) seht Ihr ein Beispiel, wie sich die Amplitude einer Flüssigkeitsschwingung mit der Zeit verringert, die zu Beginn um den Wert x ausgelenkt wurde.
Der Grund für die Amplitudenabnahme der Schwingung ist die Reibung der Flüssigkeit an der Rohrwand und in sich selbst. Durch Reibung geht Schwingungsenergie verloren, die Amplitude der Schwingung wird gedämpft. Je nach Grad der Dämpfung kann man drei Fälle unterscheiden:
Eine harmonische Schwingung entsteht, wenn - wie in der Einleitung bereits erläutert - in einem System ortsabhängige, rücktreibende Kräfte vorhanden sind. Beim U-Rohr-Schwinger ist die Schwerkraft als rücktreibende Kraft im Spiel. Nach Anregung der Schwingung wandelt sich mehrfach potenzielle Energie der Flüssigkeitssäule in Bewegungsenergie um und umgekehrt. Bei jeder Schwingung geht ein Teil dieser Energie durch Reibung verloren.
8.1 Aufgaben zu den verschiedenen Energieformen der U-Rohr-Schwingung
Für ein strömendes Medium im Rohr gibt es grundsätzlich die "laminare", die "turbulente" und "periodische" Strömungsform.
Das Kennzeichen einer laminaren Strömung ist ein gleichmäßiges Geschwindigkeitsprofil über die ganze Rohrlänge hinweg. Senkrecht dazu, d.h. auf dem kreisförmigen Querschnitt des Rohres ist die Geschwindigkeit der Flüssigkeitsteilchen am Rand des Rohres nahezu gleich null und in seinem Mittelpunkt maximal. Ursache dieses Profils ist die Zähigkeit oder Viskosität der Flüssigkeit. Die Viskosität beschreibt, wie stark sich ein fließendes Medium unter der Wirkung einer Kraft verformt. Teer oder Honig haben große Viskositätswerte, Wasser oder Gase wie beispielsweise Luft dagegen niedrige. Im Teilchenmodell kann die Viskosität auf Anziehungskräfte oder allgemein Wechselwirkungen zwischen den Molekülen zurückgeführt werden.
Kennzeichen einer turbulenten Strömung sind ungleichmäßige Wirbelbildungen in der Flüssigkeit, die von kleinen Störungen am Rohrrand oder im Strömungsquerschnitt ausgehen. In der Natur bildet jeder Wildbach eine turbulente Strömung aus. Turbulenz setzt erst ab einer bestimmten Grenzgeschwindigkeit ein, wobei in den Wirbeln Strömungsenergie gespeichert wird. Diese "Wirbelenergie" steht der Schwingung nicht mehr zur Verfügung, das turbulent schwingende System ist daher stärker gedämpft als das laminare. Durch Aufschaukelprozesse kann eine turbulente Strömung chaotisch werden; ihr Verhalten ist dann nur noch schwer vorhersagbar.
Der englische Physiker Osborne Reynolds hat Ende des 19. Jahrhunderts an Strömungen wichtige Entdeckungen gemacht. Er stellte fest, dass sich das Verhalten aller Strömungen mit Hilfe einer einzigen dimensionslosen Zahl beschreiben lässt, der nach ihm benannten Reynoldszahl Re. Sie ist ein Maß dafür, ob zufällige kleine Störungen zu Wirbeln und Turbulenzen anwachsen oder wieder abklingen. Für die Strömung von Flüssigkeiten in Rohren mit kreisförmigem Querschnitt gilt: Re = ρ di v / η. Man erkennt, dass bei gegebener Dichte ρ des Fluids und gegebenen Durchmesser di des Rohres die Reynolds-Zahl mit wachsender Geschwindigkeit v und abnehmender Viskosität η zunimmt. Sobald die Reynolds-Zahl einen kritischen Wert Rec überschreitet, kann eine vorher laminare Strömung turbulent werden. Die kritische Reynoldszahl beträgt für eine Strömung im Rohr Rec = 2320. Durch Umstellen der Formel lässt sich die kritische Geschwindigkeit vc bestimmen, ab der mit Turbulenz zu rechnen ist.
Bei der periodischen Strömung kommt neben dem örtlichen Geschwindigkeitsprofil eine zeitliche Änderung hinzu: Der Betrag der Geschwindigkeit an einem beliebigen Punkt in der Flüssigkeit nimmt innerhalb fester Zeitintervalle zu und wieder ab. Im Fall der Flüssigkeitssäulenschwingung im U-Rohr verändert sich die Geschwindigkeit des Fluids von Null in den Umkehrpunkten (unten, oben) zu einem maximalen Wert in der Mitte des Schwingungsweges (Nulldurchgang).
9.1 Aufgaben zur Strömungsform der Schwingung
Mit dem Motor, dem Pleuel-Getriebe (es wandelt eine Drehbewegung in eine lineare Bewegung um) und der Luftpumpe kann die Flüssigkeitssäule nicht nur einmalig, sondern periodisch ausgelenkt werden. Dabei wird das Luftvolumen im angekoppelten U-Rohr komprimiert und übt auf die Flüssigkeitssäule Druck aus. Die Umdrehungszahl des Motors kann durch Verändern der Motorspannung in einem ausreichenden Bereich variiert werden. Die Flüssigkeitssäule lässt sich mit einstellbarer Schwingungsdauer bzw. Frequenz anregen.
Variiert man die Frequenz der Anregung, dann antwortet das Schwingsystem mit unterschiedlicher Amplitude. Diese hat bei der Eigenfrequenz des Systems ein Maximum. Man spricht dann von Resonanz. Die im System gespeicherte Energie ist im Resonanzfall am größten. Das Verhältnis von gespeicherter Energie zur Verlustenergie nennt man Güte Q des schwingungsfähigen Systems.
10.1 Aufgaben zur angeregten Schwingung
|
|
| Copyright by Hans Joachim Ilgen seit 1950 | |