Hans Joachim Ilgen Solar Eclipse 2015 - Determining the degree of occultation of Sun

Solar Eclipse 2015 - Determining the degree of occultation of Sun

4a. Determining the degree of occultation of Sun

I got a simple but a bit inaccurate overview, by putting the chord, which was formed by the circular portion of the moon, in relation to the solar diameter. I did this with all my pictures and obtained a first approach to the occultation as a function of time.
Laborious, but more accurate is the comparison of surfaces. So I created printouts of my pictures on graph paper.
I determined the center of the sun by the method of 2 chords and their perpendicular bisectors. I have already described this geometric operation at my page of the transit of Mercury (left picture, Fig. 35). So the center of the sun was constructed.
By measuring the solar diameter I completed the covered solar disk. Later on I counted the bright boxes and substracted the result from the value of the full solar disk. Finally, I put the obtained outcome in relation to the total solar surface (right picture, Fig. 36).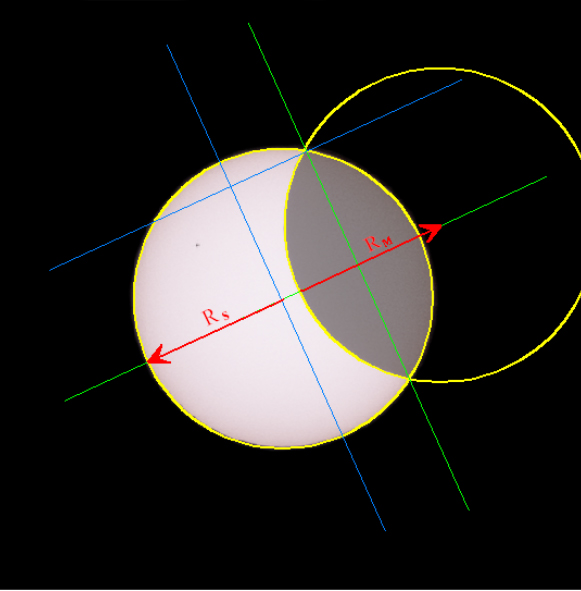

Fig. 35: Graphical center-design of Sun and Moon. Click at the image to enlarge

Fig. 36: Determining the degree of occultation of the sun graphically.
Click on the image to enlarge

In Fig. 35 it is shown additionally, how the moon's center was determined. The centers of the two celestial bodies are actually located on the mid-perpendicular of the chord, which is formed by the circular portion of the moon. By measuring the solar radius from the edge of the moon, I easily found the moon's center.

Time [hh:mm:ss]	occultation of Sun [%]	Partial eclipse [%]	Error [%]
09:35:34	5,008	94,992	4,702
09:48:28	18,544	81,456	6,650
10:01:22	35,279	64,721	4,874
10:17:02	53,902	46,098	5,389
10:29:30	68,400	31,600	5,727
10:38:22	72,624	27,376	4,647
10:54:48	59,764	40,236	5,360
11:09:20	43,119	56,881	7,090
11:20:16	24,048	75,952	7,090
11:33:40	12,425	87,575	8,538

Table 3: Solar Eclipse on March 20, 2015 as funktion of time (occultation, partial eclipse and error), observed at 'Ludwigshöhe' near Darmstadt, Gemany
(coordinats: 49.84296° N; 8.660990° E)

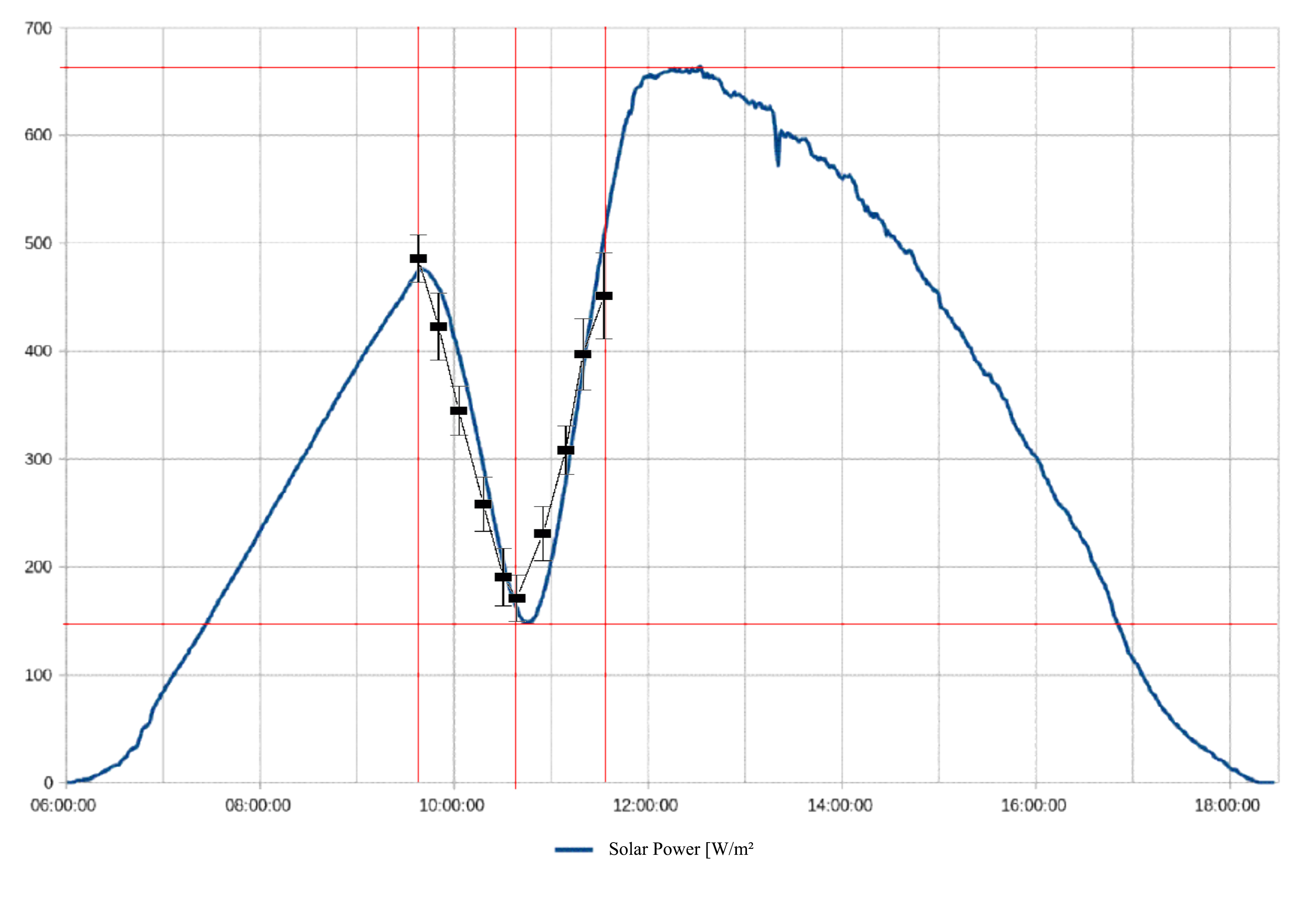
Extrapolating the measured or calculated results as a function of time, you get the course of eclipse in terms of occultation (see: Fig. 37).

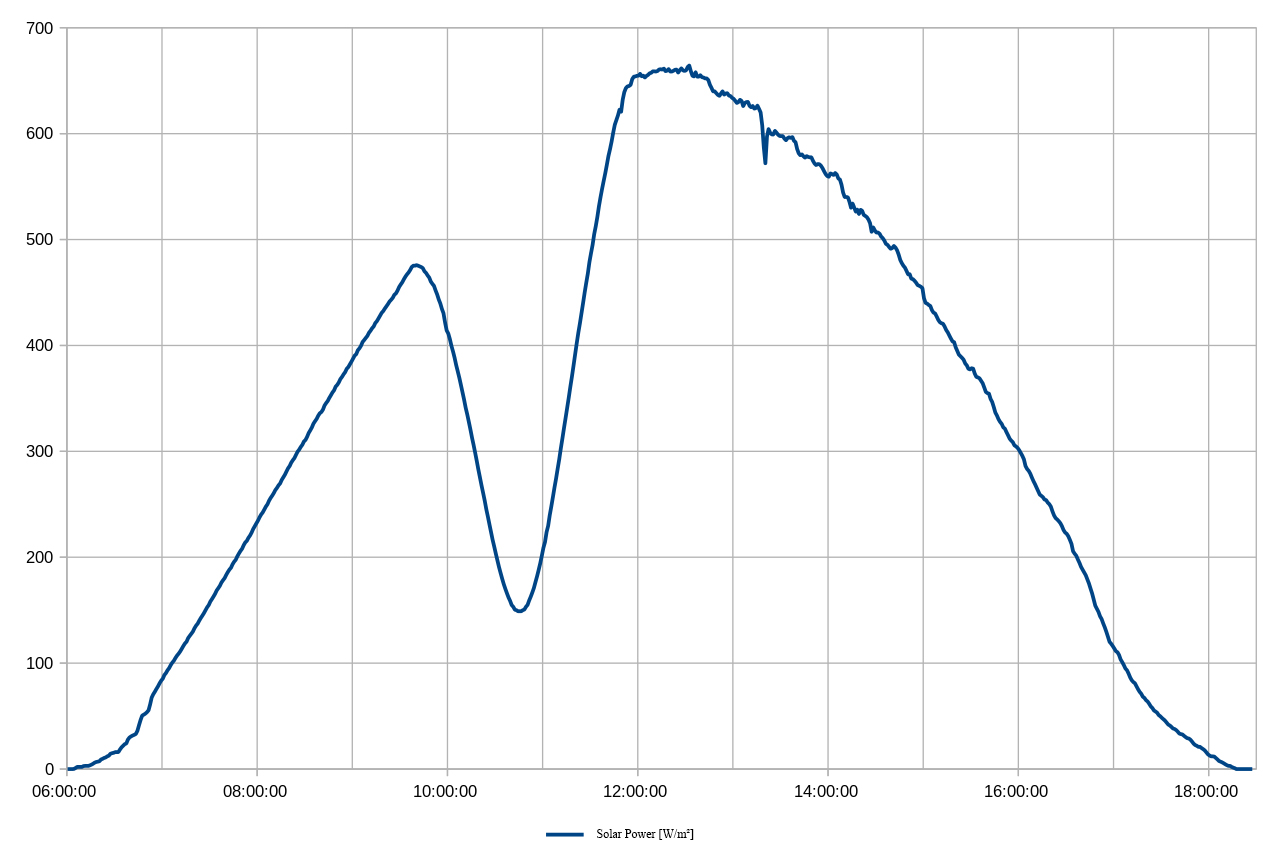
Previously various media expressed the fear, that during the Eclipse the power supply in Germany could collapse, since the Photovoltaic bears a large share of the energy supply. But this did not happen, as you will see at
German-power-net-survives-solar-eclipse
Reference: ( © Radio Deutsche Welle ).


Fig. 37: Occultation [%] of Sun on March 20, 2015 9:30 to 11:30 CET, Click at the image to enlarge	Fig. 38: Daily results of solar power in Dresden on March 20, 2015 (Occultation Dresden: 71.5%)	Fig. 39: Comparison of solar power in Dresden with my data of occultation, Click at the image to enlarge

At Wikipedia I found the course of solar power at a photovoltaic system in Dresden, Germany (sorry, this page is in German language only; see: Fig. 38). The darkening of the sun Vs(t) can be calculated using my determined occultation Bs(t) according to the relationship:

Vs(t) = 100 % - Bs(t)
I compared the images and recognized a good correlation (see: Fig. 39).

Because Dresden is about 360 km east of Darmstadt, this sets the eclipse later. The percentage of sun-occultation is lower, since the umbra east veers to the north (see: Fig. 30).

Read more at: 5. More to Explore
and get a better understanding of eclipses.

Back to top
Back to evaluating the image sequence
Back to directory